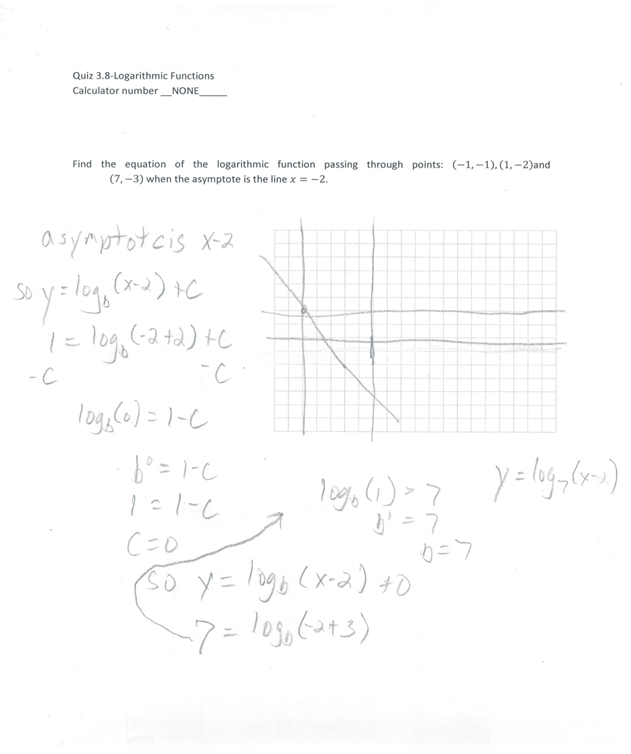
Graphing Logarithmic Functions with Transformations

Student work

Distinguished

The following Images show work which is an example of a Distinguished Student's Work. This student demonstrated clear conceptual understanding of how to graph a function using transformations. Each sketch the learner drew clearly identifies the geometric interpretation of the transformation, after which the learner states the given transformation by amending the parent function. In addition the learner included a, not-required, check to insure the solution is valid.

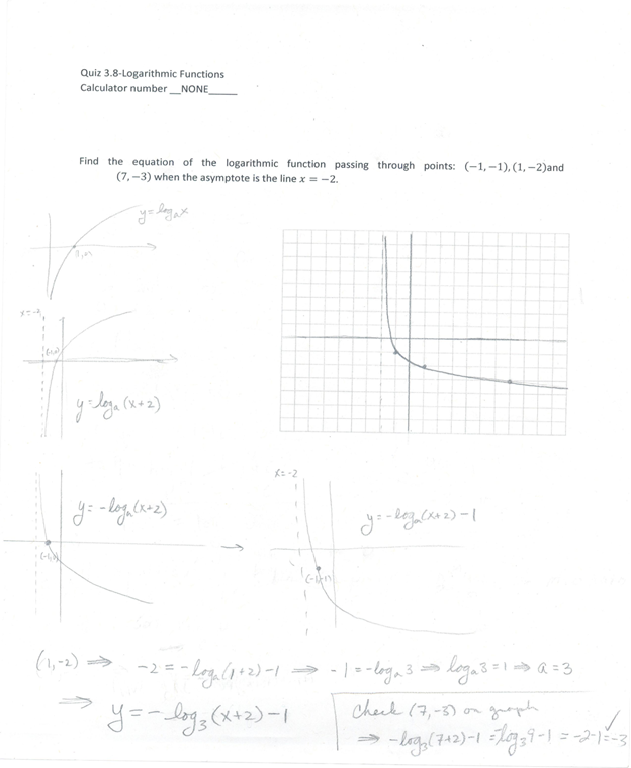
Proficient

The following Images show work which is an example of a Proficient Student's Work. This student demonstrated a mathematically logical understanding of how to graph a function using transformations. Furthermore, each mathematical calculation clearly identifies the algebraic interpretation of the transformations, using parent characteristics and the givens the learner states the equation of the new function after applying all of the givens to the parent function.

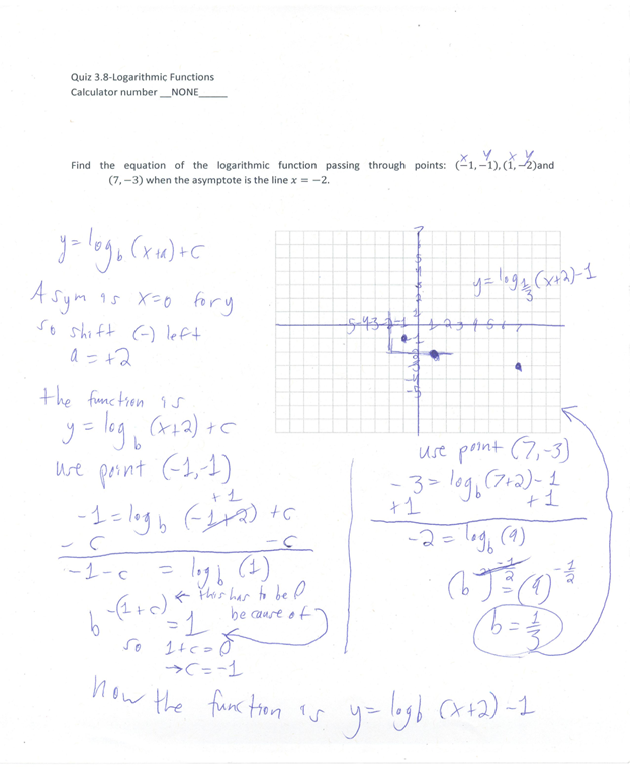
Developing

The following Images show work which is an example of a Developing Student's Work. This student demonstrated a faulty logical understanding of how to graph a function using transformations as well as inclusive of many fundamental errors. The learner's misunderstanding of concept brought forth incorrect, irrelevant, and incoherent work.