Graphing Logarithmic Functions with Transformations

procedure

Curricular Placement


This year we have covered the transformations of lines, parabolas, exponential functions, and now we are moving on to logarithmic functions.

Logarithmic and Exponential Functions Unit Time Line
Section 1 2 3 4 5 6
Topic

Exponents:

Rational and Negitive

Radical Equations

Equations with Exponents

 Exponential Functions

Logarithmic Functions

Section for Learning Experence

 Logarithmic Rules Applications of Exponential Functions
Class Time Required 2.5 Days 2.0 Days 3.0 Days 2.0 Days 1.0 Days 2.5 Days

 

Diagnostic Assessment:

The questions and answers for the oral diagnostic,

  • Has anybody heard of a Logarithmic Function before?

  • Does anybody remember what the Exponential Function looks like
    • See y= bx on the graph below.
  • Which line do you reflect a function over to find its inverse image?
    • The line y= x.
  • If an Exponential Function is the inverse to the Logarithmic Function what should the
    image of a Logarithmic Function look
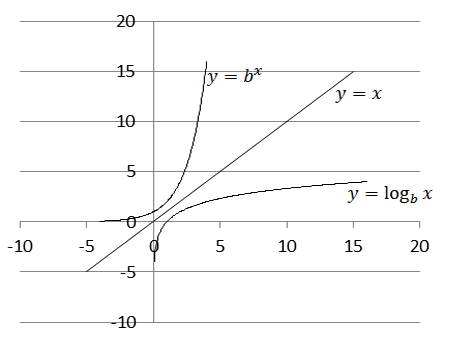
    • See y= logb(x) on the graph below.




 

Anticipatory Set:


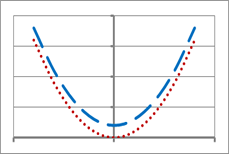
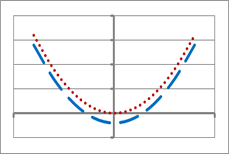
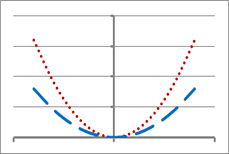
Using a graphing calculator graph and identify the change on y= x2 under the given transformation for yi=f(x).

y1= x2+2 y2= x2-2
shift up two units Shift two units down
y3= (x+2)2 y4= (x-2)2
shift left two units shift right two units
y5=(1/2)x2 y6= (5/2)x2
compresses image strech the image
y=x^2 key y=x2 y=y_i graph key y= yi

 

Input:

The input for the lesson will be a lecture on logarithmic functions and the effects of transformations on logarithmic graphs.

  • What is the difference between a logarithm and an exponent?
    • A logarithm is an exponent
  • What is the difference between Exponential and Logarithmic form?
    • x= by is in exponential form.
    • y= logb(x) is in logarithmic form.
  • How does one find the inverse of a function algebraically?
    • Switch the x and y in a given equation and then solve it for y.
  • What base do common logarithms have?
    • Common logs have a base of 10.
  • What base do natural logarithms have?
    • Natural logs have a base of e.
  • Why do we change from Logarithmic form into Exponential form when graphing Logarithmic Functions?
    • It is more efficient to represent x as a function of y, and then let the values for y vary.
  • What is the difference between a function of “x” and a function of “y”?
    • With a function of “x” one lets the x values vary. With a function of “y” one lets the y values vary.
  • If the base of a Logarithm is greater than one, does the function increase or decrease?
    • Logarithms with a base greater than one increase.
  • If the base of a Logarithm is greater than zero but is also less than one, does the function increase or decrease?
    • Logarithms with a base greater than zero but less than one decrease.
  • What point is a characteristic or featured in a Logarithmic Function?
    • The point (1,0).
  • What is the domain of a Logarithmic Function?
    • DOM[f(x)]={x | x € (0,infinity)}.
  • What is the Range of a Logarithmic Function?
    • RNG[f(x)]={y=f(x) | y € (negitive infinity, infinity)} or all real numbers.
  • Does a Logarithmic Function have an Asymptote?
    • Yes, the parent function will never cross the line x = 0, or the y-axis.

 

Model:                  

Since the input for the lesson is a lecture on logarithmic functions and the effects of transformations on logarithmic graphs the Guided note packet issued at the beginning of the unit will be utilized for the modeling the conceptual aspects of the lesson, through interrogatives and examples.

Example 1, to write 2= log5(25) in exponential form. FIRST-Remember that, y= logb(x) <--> x= by

So given example 1, --> 2= log5(25) <--> {25= 52}.

 

Example 2, to write 3= 91/2 in logarithmic form. FIRST-Remember that, x= by <--> y= logb(x)

So given example 2, --> 3= 91/2 <--> {1/2= log9(3)}.

 

Example 3, to solve 2= log12(x) for x. FIRST-Remember that, y= logb(x) <--> x= by

So given example 3, 2= log12(x) <--> x= 122 --> {x=144}.

 

Example 4, to solve 1/2= logx(16) for x. FIRST-Remember that, y= logb(x) <--> x= by

So given example 4, 1/2= logx(16) <--> 16= x1/2 --> {x= 256}.

 

Example 5, to evaluate logsqrt(3)(9). FIRST-Remember that, y= logb(x) <--> x= by

So given example 4,logsqrt(3)(9) <--> y= logsqrt(3)(9) --> 9= (31/2)y --> 32=3y/2 --> {y=4}.

 

Lastly, graph the three examples at the end of the logarithmic function section in the guided note packet. Be sure to allude to the fact that one must first change the given function from logarithmic form to exponential form, then pick an arbitrary set of values for y and not x then solve the new function of “y” for x. In general the set A={-3, -2, -1, 0, 1, 2, 3} is sufficient for the range or the values for y. After the values for y have been determined, substitute them in to the function of y and then solve each equation for the corresponding value of x. After all the values for y have been substituted in make a table of values and plot the points.

 

Guided Practice:                    

A Note Sheet, with two examples, is issued to the learners at the end of the lecture. This worksheet provides an opportunity for the learners further their own conceptual understanding of how to graph logarithmic functions using transformations by following along and completing the given task at hand with support and guidance. (Please note a detailed key Click here).

 

Independent Practice:

A Worksheet with two examples is assigned for homework. Remember the assignment is given either a complete (reasonable effort, both questions answered) or incomplete (less-than reasonable effort, only one or no questions answered) grade. (Click here for a completed worksheet).

 

Closure:

An informal discussion about the geometric translations due to algebraic transformations. Also a Handout will be given which states the effects of transformations.

 

Formative Assessment:

The learner is given a ten minute quiz, Quiz #3.8 approximately on the day the homework is corrected and collected.